Entenda como funciona a estratégia que virou fenômeno nas redes sociais nos últimos dias
O vídeo que ensina um método de “multiplicação japonesa” foi reproduzido mais de 100 milhões de vezes desde o dia 11 de novembro no Facebook, onde teve mais de 2 milhões de compartilhamentos.
Na realidade, é um sistema de multiplicação com linhas que viralizou mais de uma vez, mas com outros nomes: também foi chamado de multiplicação maia, mas como já explicamos é impossível que fosse maia, a não ser que as linhas se referissem a abelhas.
https://www.facebook.com/didyouknowpage1/videos/1549535068487238/
Ainda assim, gostamos muito das maneiras diferentes de multiplicar e, ainda que duvide muito que no Japão ensinem dessa forma, veremos como se faz, usando como exemplo uma multiplicação de dois números de duas cifras, 32×12. Depois tentaremos generalizá-lo e finalmente, aproveitando que eles não me leem, veremos o exercício que certamente colocarei para meus alunos de matemática. Logicamente, também o mais interessante de todos esses truques: explicar por que funciona.
1. Faço dois grupos de segmentos paralelos: no primeiro coloco tantas linhas como o número de dezenas completas do primeiro fator, no segundo tantos segmentos como o número de unidades. Ou seja, no caso do exemplo, três segmentos em cima e dois embaixo, porque o primeiro fator é 32. Menos mal que é 32, se fosse 87 pareceria um código de barras.

2. Faço outros dois grupos de segmentos paralelos, em outra direção. No primeiro coloco tantas linhas como a quantidade de dezenas completas do segundo fator (um) e no segundo, as unidades (dois).

3. Conto os pontos de intersecção dos segmentos. Se o fizer com todo o cuidado e tiver sorte, terminei: os que estão à direita são 4, esse é o número das unidades; os que estão nos dois cantos do centro (tanto em cima como embaixo) são o número das dezenas, no caso desse exemplo temos seis em cima e dois embaixo, ou seja, 8 dezenas completas; os três que restam à esquerda somam a cifra das centenas. Voilà, 32×12=384. Que alegria! E o fiz quase tão rápido quanto com a calculadora do celular (na verdade, não).
4. E se algo sair errado? Ao fazer 34×12, no lugar de 8 pontos na parte central aparecem 10, o que indica que o produto tem 10 dezenas. Certo, então fico com uma, não? 10 dezenas formam uma centena e, portanto, o resultado será 408:
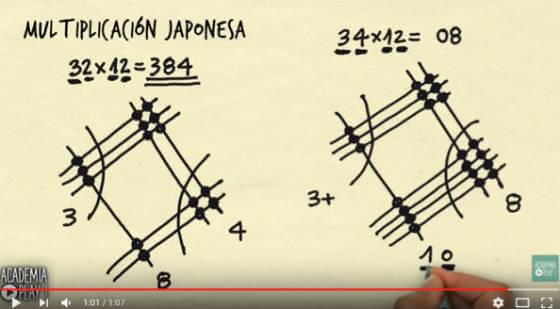
Por que funciona? (Atenção alunos): porque decompus meus números de duas cifras em dezenas e unidades, e quando multiplico unidades por unidades obtenho unidades, quando multiplico unidades por dezenas, obtenho dezenas, e quando faço dezenas por dezenas obtenho centenas, capisce?
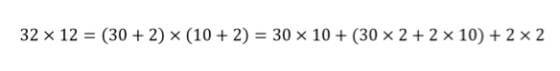
Para desenvolver os parênteses apliquei a propriedade distributiva, e no parêntesis central do resultado enquadrei o que fica no centro do diagrama de retas: 3×2=6 pontos e 2×1=2 pontos, 8 pontos no total. Na realidade são 30 vezes 2 (ou duas vezes 30, dá no mesmo apesar de não ser o mesmo) e duas vezes 10, no total 60 mais 20 são 80, como sempre foi.
Ainda resta esclarecer uma coisa e é como posso saber o resultado de uma multiplicação cruzando linhas e contando pontos. É a verdadeira magia desse método, que não é preciso saber as tabelas de multiplicação para calcular os produtos.
Mas isso não é magia, somente matemática: é a mesma relação que se dá em qualquer disposição retangular (matriz). Sempre encontramos tantos elementos como o número de fileiras multiplicado pelo número de colunas. Para dar um exemplo, em um edifício de quatro andares existem cinco varandas por andar, no total teremos 20 varandas. Eu gosto muito dessas relações e as coloco no Instagram com a hashtag #xEsVeces. Não quero ganhar seguidores (só um pouco), é para ver se você também gostaria de tentar.
Isso serve às escolas?
Muitos dos comentários do vídeo original e, me adianto, também dos desse artigo, dirão que devemos ensinar a multiplicar dessa forma nas escolas. Não concordo. Esse truque é pura mecânica e só resolve multiplicações de números de poucas cifras (e de cifras baixas), sendo também muito lento.
Ser lento não precisa ser um problema, se servir para entender melhor o processo e for possível ser exportado para resolver problemas do mundo real. Por essa última colocação podemos utilizá-lo no ensino para pedir a alunos com certa maturidade que tentem explicar por que funciona (como eu certamente farei ao final de minha matéria).
Não estou querendo com isso defender os algoritmos tradicionais que também são ensinados mecanicamente na escola. Deveríamos utilizar procedimentos que possam ser compreendidos, sobre números que os alunos possam imaginar, e sempre pedindo previamente uma estimativa, um cálculo aproximado de qual será o resultado, para que o comparem com o resultado obtido posteriormente e dessa forma sirva para aprender alguma coisa. Realizar operações enormes sobre números igualmente grandes não contribui para nada, mas essa é outra história, e a contaremos em outra ocasião.
* Vídeo disponível no youtube
Fonte: El País Brasil



